Introducción: El Papiro Rhind es el conocimiento de todos los secretos oscuros
“Un estudio completo de todas las cosas, una reflexión de todo lo que existe, el conocimiento de todos los secretos oscuros”. Con esta frase es que, el escriba Ahmes, comienza lo que sería el mejor texto escrito sobre cómo eran las matemáticas egipcias hace 4000 años. Este documento, hoy es conocido como el Papiro Rhind o Papiro de Ahmes, el cual contiene 87 problemas matemáticos y fue escrito en el 1650 a.C. El propósito de este artículo es que conozcas y aprendas cómo eran las matemáticas egipcias, por eso está bosquejado de la siguiente forma:
- Cómo surgen las matemáticas egipcias
- La estructura del Papiro Rhind (Autor, datación, museo y estructura)
- Cómo eran las matemáticas egipcias (Sistema de numeración, multiplicación y división egipcia)
- Las fracciones: el dolor de cabeza de los egipcios (Unidades de medida, fracciones de Horus y fracciones egipcias)
- Resolución de problemas del papiro Rhind.
Cómo surgen las matemáticas egipcias
Egipto fue un pueblo próspero y poderoso, destacado en ciencia y obras monumentales. Las grandes pirámides, como la de Keops, son un claro ejemplo de su grandeza. Construida entre el 2550 y 2527 a.C., con 2.3 millones de bloques de piedra, cada uno pesando alrededor de dos toneladas. Resulta sorprendente que exista un papiro que revele los secretos de su construcción. Estudiar este documento nos permitiría desvelar los conocimientos detrás de estas impresionantes estructuras.

Para saber el origen de las matemáticas, que dieron lugar al amplio desarrollo arquitectónico de la civilización egipcia, debemos remontarnos a los orígenes de Egipto. Como dijo el historiador Heródoto, Egipto es un regalo del río Nilo. Se sabe que existía antes del 4000 a.C. y que la mayor parte de la población vivía de la agricultura gracias a la fertilidad brindada por el río Nilo, también vivían de la pesca y la caza.
Cada año, en los meses de julio a noviembre, el río Nilo se desbordaba ocasionando dos hechos: fertilidad de las tierras aledañas y destrucción. Estos desbordamientos favorecieron la agricultura pero a la vez representaba un desafío pues tenían que contener el agua para evitar las destrucciones, por eso los egipcios se hicieron hábiles en la construcción de canales, embalses y cercos. Esto impulsó el desarrollo de la geometría (medida de la tierra) y la aritmética. Así es como en tiempos de adversidad el ser humano se adapta y aprende.
La estructura del Papiro Rhind
Miles de años pasaron desde el nacimiento de las matemáticas egipcias hasta que el escriba Ahmes redacta lo que parece ser una guía didáctica para resolver problemas matemáticos. El papiro Rhind es una recopilación de un texto más antiguo, de 200 años antes del mismo.

Año de descubrimiento, primer dueño y lugar de exhibición: El papiro fue descubierto en el siglo XIX y adquirido por el egiptólogo Alexander Henry Rhind en el año 1858, fue encontrado en las ruinas de la antigua ciudad de Tebas. Rhind murió 5 años después, y el papiro fue a parar al Museo Británico donde hoy día es exhibido. Puedes ingresar a la página web oficial de British Museum, haciendo clic aquí, y consultar por ti mismo el contenido del papiro Rhind.
Tamaño, datación, autor: El papiro tiene las siguientes dimensiones: 6 metros de largo y 33 centímetros de ancho. Fue escrito alrededor del año 1650 a.C. y el autor es el escriba Ahmes. El conocimiento que se expone en el papiro corresponde a tiempos anteriores a 1650 a.C.
Estructura y escritura: Consta de 87 problemas matemáticos y su resolución, en escritura hieriática. Los problemas pueden clasificarse en: Aritmética básica, multiplicación y división de fracciones, cálculo de áreas, volúmenes, progresiones, repartos proporcionales, regla de tres, ecuaciones lineales y trigonometría.

A continuación te muestro una tabla con los problemas del papiro, categorizados según Richard J. Gillins en su libro «Matemáticas en tiempos de los faraones»:

Cómo eran las matemáticas egipcias
Cómo escribían los números los egipcios
El sistema de numeración egipcio era de base 10 y no posicional. Los egipcios utilizaban 7 jeroglíficos, uno para representar la unidad, otro para la decena, otro para la centena, y así sucesivamente hasta la unidad de millón.

Repetir tres veces el símbolo correspondiente al 1, indicaba el número 3.

Repetir dos veces el símbolo correspondiente al 10, indicaba el número 20..

Repetir dos veces el símbolo correspondiente al 1000, indicaba el número 2000.

El problema era que, para representar algunos números, era necesario emplear demasiados símbolos, por lo que los egipcios inventaron un sistema alternativo: el sistema hierático. El cual es un estilo simplificado y estilizado de los jeroglíficos. En este sistema se introdujo un símbolo distinto para cada unidad, para cada decena, para centena y los millares.

En las siguientes dos representaciones del mismo número, podemos ver como con el sistema hierático queda representado con solo 3 símbolos, mientras que con el anterior era necesario usar 7 símbolos.

El método egipcio para multiplicar: La duplicación
Como pudimos ver en su sistema de numeración, las matemáticas egipcias eran esencialmente aditivas, de ahí que su método para multiplicar tenga como fundamento la adición. El método egipcio para multiplicar es el más antiguo, para explicarlo tomaremos como ejemplo el siguiente producto 80×14. Consiste en los siguientes pasos:
- Elaborar una tabla encabezada por dos números: en la izquierda el factor de mayor valor absoluto y en la derecha siempre comenzaremos con el número 1.
- Duplicar ambos números: Multiplicar por dos reiteradamente mientras el número de la derecha no sobrepase al segundo factor (no sobrepase a 14).
- Seleccionar números de la columna derecha: La suma de los números debe ser igual al segundo factor (en este caso a 14).
- Sumar las cifras de la izquierda: Sumaremos los números de la columna izquierda correspondientes a los números seleccionados anteriormente de la columna derecha.
El resultado de 80×14 es la suma de las cifras señaladas de la columna izquierda, es decir, 160+320+640 = 1120 (Haz clic aquí para ver un short sobre esto)
El método egipcio para dividir
La forma en que los egipcios dividían es muy interesante. Si queremos dividir a entre b, la idea del egipcio consiste simplemente en tomar el número de b y de partes de b que sumen a. Como hicimos anteriormente, lo haremos con un ejemplo: 67/5, tomaremos el número de 5 y partes de 5 que sumados den 67.
- Elaborar una tabla encabezada por dos números: en la izquierda colocaremos el divisor (es decir, el 5). En la derecha siempre comenzaremos con el número 1.
- Duplicar ambos números: Mutiplicar por dos reiteradamente mientras el número de la izquierda no sobrepase al dividendo (en este caso no debe sobrepasar a 67).
- Seleccionar números de la columna izquierda: Se deben seleccionar aquellos números que al sumarse sea igual al dividendo (es decir a 67) o, en su defecto, que se acerque lo más posible a 67 sin sobrepasarlo.
- El cociente es la suma de las cifras de la derecha: Sumaremos los números de la columna derecha correspondientes a los números seleccionados anteriormente de la columna izquierda.
El resultado de 67/5 es la suma de las cifras señaladas de la columna derecha más el residuo, es decir, 1+4+8 + 2/5 = 13 + 2/5.

Las fracciones: El dolor de cabeza de los egipcios
Las fracciones quizás fueron la gran limitante que tuvo la matemática egipcia, los cálculos complicados con fracciones impidieron probablemente el desarrollo de una aritmética y un álgebra avanzadas. La notación egipcia para las fracciones era fastidiosa e inadecuada para el cálculo. Esto provocó que su forma de denotar y realizar cálculos con fracciones fuera casi completamente ignorada por las culturas posteriores.
Para entender cómo los egipcios veían las fracciones y realizaban sus cálculos, en primer lugar, debemos saber cuáles eran las unidades de medida que los egipcios utilizaban, especialmente el Heqat (unidad de medida de volumen).
Unidades de medida en Egipto
Las unidades de medida principales, en Egipto, fueron las siguientes:
Unidades de longitud: El dedo, equivalente a 1.86 cm, era la unidad principal de longitud, le seguían los múltiplos del dedo, como el palmo (equivalente a 4 dedos), la mano (equivalente a 5 dedos), el puño (equivalente a 6 dedos), etc.

Unidades de superficie: La unidad básica para medir superficies en Egipto era el sechat, que equivale a un cuadrado de 100 codos de lados, lo que sería en medidas actuales 2735,29 m². Del sechat derivan otras medidas, que son submúltiplos, como el remen (equivalente a la mitad de un sechat) y un sa (equivalente a una octava parte de un sechat).

Unidades de volumen: La unidad de capacidad de volumen era el Heqat y era utilizada especialmente para medir el trigo y la cebada (cereales). El heqat era representado por el ojo de Horus; equivalía a 4.8 litros. De este derivan múltiplos como el doble-heqat (equivalente a dos heqat), el Ipet (equivalente a 4 heqat) y el jar (equivalente a 20 heqat). También se consideraban los submúltiplos, dividiendo el Heqat por 2 de forma sucesiva, obteniendo 1/2 , 1/4, 1/8, 1/16, 1/32 y 1/64 de heqat.

Fracciones Ojo de Horus (Fracciones de un Heqat)
El heqat como unidad completa era representado por el ojo de Horus, y las 1/2 , 1/4, 1/8, 1/16, 1/32 y 1/64 de heqat eran representadas por partes específicas del ojo de Horus. Recordemos que un Heqat = 4.8 litros, entonces 1/2 heqat = 2.4 litros, 1/4 heqat = 1.2 litros, 1/8 heqat = 0.6 litros, 1/16 heqat = 0.3 litros , 1/32 heqat = 0.15 litros , 1/64 heqat = 0.075 litros.

Cuando se medía el grano en heqats se usaban las fracciones Ojo de Horus. También estaba la unidad de medida llamada Ro definida como 1/320 de heqat; equivalente a 0.015 litros. Para medidas inferiores a 1/64 de heqat, se utilizaban múltiplos de Ro. El simbolo de Ro es el siguiente:

Luego este símbolo que originariamente representaba 1/320 de heqat, pasó a representar la idea de fracción y se solía escribir encima del número para indicar la fracción que se quería. Por ejemplo:

Nótese que solo usaban fracciones con numerador igual a 1. También se define otra unidad de medida que podemos encontrar en el papiro Rhind, llamada huno, la cual es igual a 1/10 de heqat, es decir, 1 huno = 0.48 litros. Se utilizaba especialmente para medir cerveza y agua. Aquí tienes una tabla con las medidas de volumen:

Fracciones egipcias
Se denomina fracción egipcia a cualquier suma de fracciones unitarias distintas, es decir, fracciones con numerador 1 y denominadores distintos entre sí. Esto es así porque los egipcios solo utilizaban fracciones con numerador 1 y denominadores distintos. Por eso el papiro Rhind contiene al principio, una tabla en la que se expresan las fracciones de la forma 2/n (donde n toma valores impares entre 5 y 101, es decir, 5 ≤ n ≤101) como suma de fracciones con numerador 1 y denominadores distintos. La tabla luciría así para nosotros:
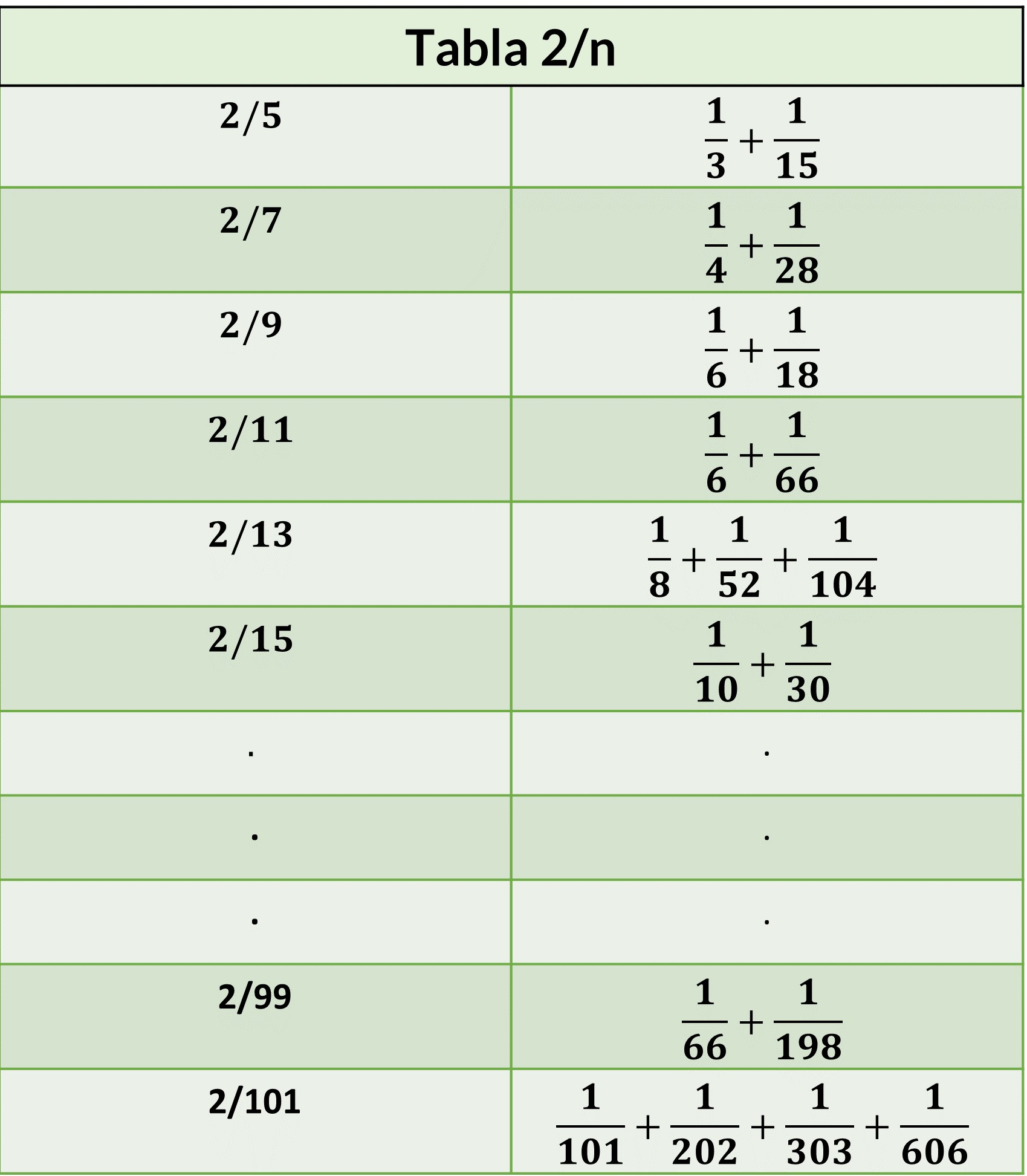
De esa manera, un egipcio, en vez de trabajar con la expresión 2/5, lo hacía con su descomposición 1/3 + 1/15. El escriba también suministra una tabla en la que descompone fracciones de la forma n/10 en suma de fracciones con numerador 1 y denominador distinto.
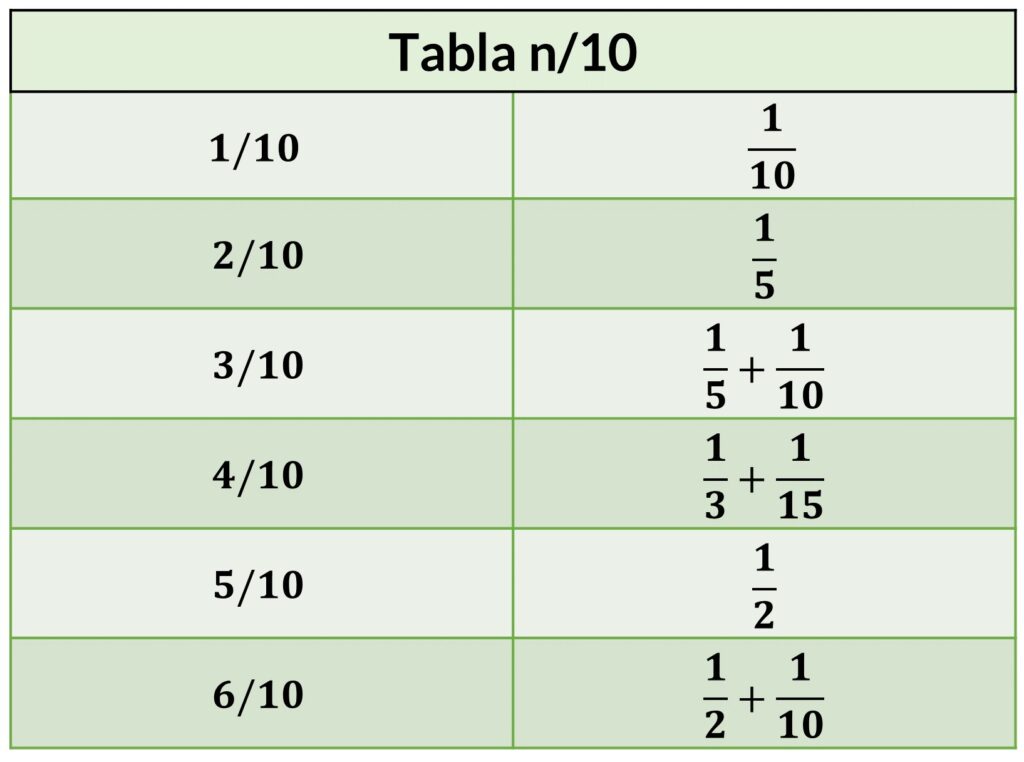
Estas tablas tuvieron una función análoga a las que tienen las tablas de integrales, de derivadas o de logaritmos para nosotros, la cual es proveer resultados que serán útiles en cálculos posteriores y evitarnos ciertos procedimientos que pueden ser engorrosos. El escriba Ahmes usa los resultados de la tabla 2/n y n/10 en problemas posteriores, por eso las ubica al principio del escrito.
¿Por qué los egipcios solo utilizaban fracciones unitarias?
Como te habrás dado cuenta, los egipcios solo utilizaban fracciones unitarias en sus cálculos (con algunas excepciones, como el 2/3) y quizás te estés preguntando por qué. La realidad es que el escriba Ahmes no presenta una justificación de las fracciones que utiliza, no explica, por ejemplo, por qué descompone 2/5 como 1/3 + 1/15 y no simplemente como 1/5 + 1/5.

¿Por qué el escriba Ahmes decidió colocar dichas fracciones en las tablas? ¿Se obtuvieron mediante un método o procedimiento específico, o a través del ensayo y el error? Existen diversas opiniones sobre ello, aquí te presentamos la que consideramos que tiene mayor concordancia con el oficio del escriba egipcio y con el conocimiento de la época.
Debemos recordar que sobre el escriba egipcio descansaba, en parte, la responsabilidad del buen funcionamiento del Estado y eran los encargados de inscribir, clasificar, contabilizar y copiar, utilizando varios tipos de escritura. Así que lo más probable es que el escriba fue escribiendo la tabla a medida que fue enfrentando diversas necesidades en su trabajo, específicamente la necesidad de repartir bienes. Era importante realizar la repartición de la forma más eficiente posible, para ahorrar tiempo y que no se desperdicie nada.
Repartición de panes por el escriba Egipcio
Ejemplo: ¿Cuál es la mejor forma de repartir 2 panes entre 5 personas?
Lo primero que quizás harías, con los conocimientos actuales, es fraccionar cada pan en cinco partes iguales y entregarle a cada persona 2/5 partes. Sin embargo, los egipcios efectuaban el reparto por medio de aproximaciones sucesivas, realizando el reparto en varias fases. Distinto a como lo hacemos hoy día. Estas aproximaciones sucesivas se realizan de la siguiente forma:
- Se compara la cantidad de panes con la de personas; si hay igual cantidad de panes que de personas se entregará una unidad de pan completa a cada uno.
- Si hay menos panes que personas entonces se fraccionan los panes en dos; si dividimos 2 panes en dos, tendríamos 4 pedazos de pan. Aún no alcanza para las cinco personas.
- Fraccionar los panes en tres, si dividimos 2 panes en tres, tendríamos 6 pedazos de pan de tamaño 1/3 cada pedazo. Es suficiente para entregarle a 5 personas 1/3 de pan, sin embargo sobra 1/3.
- Este residuo de pan, es dividido en 5, lo cual sería 1/5 de 1/3, lo cual es 1/15 del pan completo.
De manera que a cada persona se le entregó 1/3 + 1/15 de pan.

Problemas del Papiro Rhind
Repartir panes
Los primeros problemas consisten en la repartición de 1, 2, 6, 7, 8 y 9 hogazas de pan entre 10 hombres. En estos problemas, Ahmes coloca los resultados y luego procede a comprobarlos. El escriba utiliza los resultados habidos en las tablas 2/n y n/10 colocadas al principio del papiro. Presentaremos el problema 3 y su solución, tal y como lo hizo el escriba Ahmes hace 4000 años.
Problema 3: Repartir 6 panes entre 10 hombres
El resultado que nos da Ahmes es el siguiente: 1/2 + 1/10. Entonces a cada uno de los 10 hombres se le otorgó la mitad de un pan más la décima parte del mismo. El escriba procede a comprobar este resultado multiplicándolo por 10.
Mutiplicación de fracciones
Las multiplicaciones de fracciones se trabajan en los problemas del 7 al 20. En estos ejercicios se utilizan las tablas dadas por Ahmes al inicio de papiro, para sumar los resultados parciales y para descomponer fracciones en suma de fracciones unitarias.
Problema 9: Multiplica (1/2 + 1/14) por (1 + 1/2 + 1/4)
En este problema, Ahmes multiplica (1/2 + 1/14) por cada término del multiplicador (1 + 1/2 + 1/4) y luego suma los resultados parciales. Lo hace de la siguiente manera:
Ecuaciones lineales
Problema 26: Una cantidad y un cuarto de ella da un total de 15. ¿Cuál es la cantidad?
Es lo mismo que resolver la ecuación Χ + Χ/4 = 15, la cual se resuelve con nuestro método actual de la siguiente manera: Χ + Χ/4 = 15 ⇒ 4Χ + Χ = 4 (15) ⇒ 5Χ = 60 ⇒ Χ = 12
Sin embargo, los egipcios la resolvían de la siguiente forma:
- Tomaban a X = 4 como aproximación inicial. Ya que esto haría que X/4 sea igual a 1. Pero, observemos que si X = 4, entonces X + X/4 ≠ 15.
- Si X = 4, entonces X + X/4 = 4 + 4/4 = 5. Por tanto se procede a encontrar un número N, tal que N×5 = 15. En este ejercicio N = 3.
- Por último se debe multiplicar N por el valor dado a X inicialmente. N×X = 3×4 = 12. De manera que X = 12, es la solución al problema 26 del papiro Rhind.
Cálculo de áreas
Problema 50: Calcular el área de un campo circular que mide 9 jet de un lado a otro.
Hoy día solucionamos este problema de una forma muy sencilla. Simplemente podemos hacer uso de la formula para calcular el área de un circulo: A= π×r². Si el diámetro del círculo mide 9, entonces su radio mide la mitad; 4.5. Sustituyendo en la fórmula tenemos que A = π×(4.5)² = 63.618.
Sin embargo, los egipcios no conocían esta fórmula porque desconocían el número π. La forma en que calculaban el área de un circulo era construyendo el círculo inscrito en un cuadrado de lado d, donde d es el diámetro del círculo. Dado que el área del cuadrado de lado d es visiblemente mayor que el área del círculo de diámetro d, el escriba aproximaba el área del circulo al área del cuadrado de lado d-1.
«Resta al diámetro 1/9 del mismo, que es 1. La diferencia es 8. Ahora multiplica 8 veces 8, que da 64. Este es el área del círculo»



