Introducción
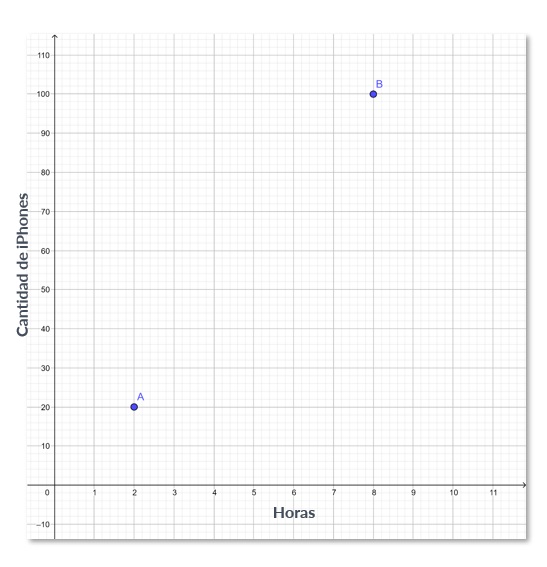
Imagina que eres gerente de una fábrica de Apple. Sabes que en 2 horas se producen 20,000 iPhones y en 8 horas se realizan 100,000 iPhones. Si el número de iPhones producidos tiene una relación lineal con las horas trabajadas, ¿Cuántos iPhones se fabricarán en 5 horas?

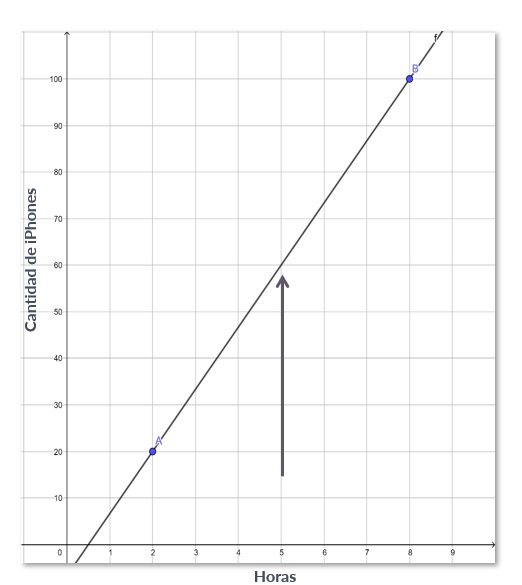
Estos son los puntos conocidos de la tabla anterior, sabiendo que el comportamiento es lineal entonces podríamos obtener una función f(x) que “pase” por los puntos conocidos.
Esta función es ƒ(x) = 40000⁄3 x – 20000⁄3 con esta función podemos estimar el número de iPhones producidos en 5 horas, simplemente evaluando ƒ(5) = 40000⁄3 (5) – 20000⁄3 = 60,000 iPhones fabricados.
¿Qué es la interpolación?
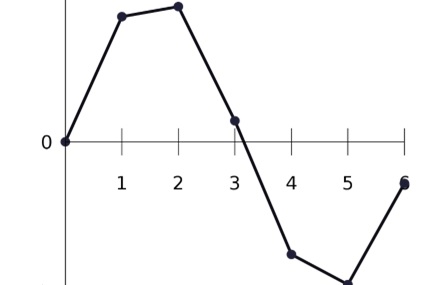
Lo que acabamos de hacer en el ejemplo anterior es un caso de interpolación lineal, la interpolación implica descubrir un cierto patrón en un conjunto de puntos, para luego obtener una curva que “conecte” los puntos conocidos y nos permita estimar un valor entre dos puntos.
Teorema de Aproximación de Weierstrass
El teorema expresa que: Dada una función real continua cualquiera, definida en un intervalo cerrado y acotado, puede ser aproximada tanto como se quiera por un polinomio.

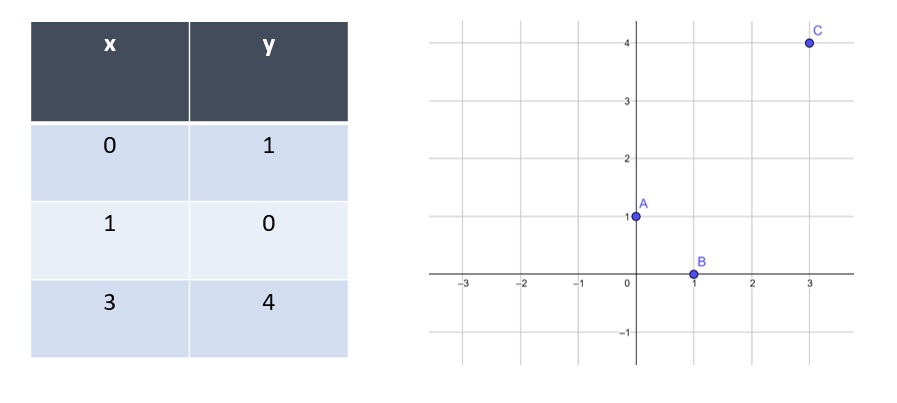
Si desconocemos la expresión analítica de una cierta función g(x) pero sí conocemos el valor de g(x) en algunos puntos, podremos hallar una función polinómica P(x) que se aproxime a g(x) tanto como se desee , en el intervalo que nos interesa.
Ejemplo
¿Cómo podemos calcular un valor intermedio entre (0, 1) y (1, 0) ó entre (1, 0) y (3, 4)?
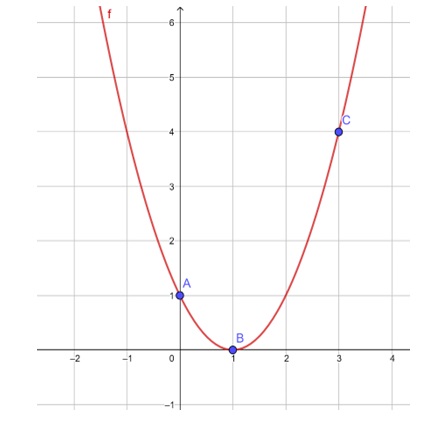
El polinomio P(x) = x² – 2x + 1 es el polinomio interpolante para los tres puntos dados. Pero ¿Cómo hallar los polinomios interpolantes?
En otros posts abordaremos distintos métodos de interpolación, como:
- Interpolación lineal
- Interpolación cuadrática
- Interpolación de Lagrange,
- Interpolación de Hermite
- etc.