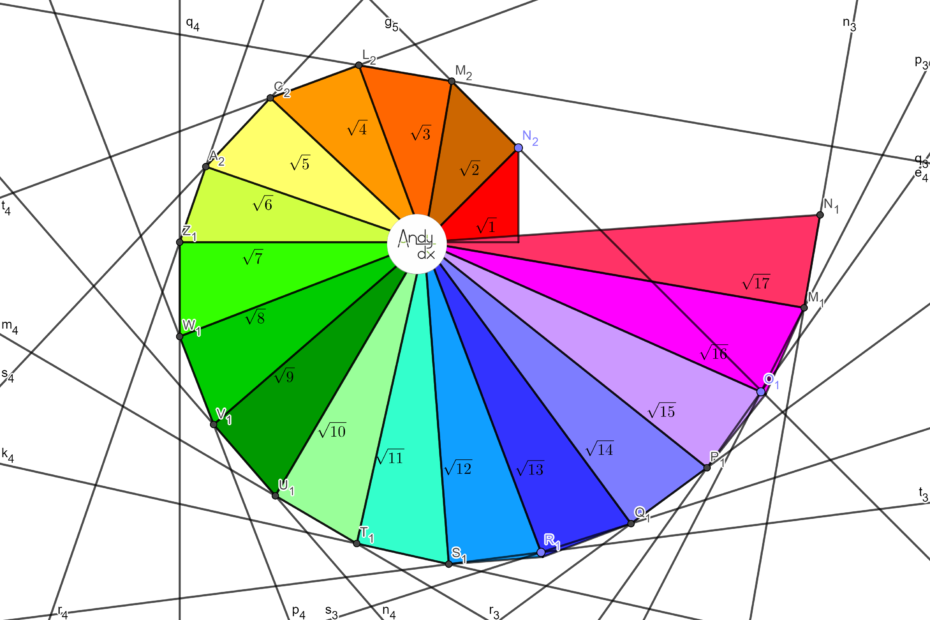
Hoy hablaremos de un objeto geométrico que es hermoso, pero además de hermoso, es simple, y debido a eso aparece en numerosos libros de texto. Me refiero a la Espiral de Teodoro, también conocida como la caracola pitagórica. También suelen referirse a ella como Espiral Pitagórica o Espiral de raíces cuadradas. Todos estos nombres expresan algunas características de este objeto geométrico: Uno hace alusión a su autor, Teodoro de Cirene, y otro al teorema que justifica su construcción, el teorema de Pitágoras. Pero antes conviene que sepas quién fue Teodoro de Cirene.
Teodoro de Cirene: tutor de Platón
Teodoro de Cirene (465 a. C. – 398 a. C.) fue un filósofo y matemático griego nacido en Cirene, actual Libia, es conocido por su trabajo con los números irracionales, él probó la irracionalidad de las raíces de los números enteros no cuadrados, es decir, las raíces de 3, 5, 6, 7… hasta el 17. No probó la irracionalidad de raíz cuadrada de 2 porque para su tiempo ya se tenían pruebas de su irracionalidad.
Teodoro fue alumno del famoso filósofo presocrático Protágoras, la mayor parte de su vida estuvo en Atenas donde pudo conocer a los famosos filósofos Sócrates y a Platón, de hecho, Teodoro enseñó matemáticas a Platón, y es por este último y su diálogo Teeteto que sabemos que Teodoro demostró la irracionalidad de las raíces cuadradas de 3, 5, 6, 7… 17.

¿Qué es la espiral de Teodoro?
La espiral de teodoro, es una espiral construida a partir de triángulos rectángulos contiguos, (uno encima de otro consecutivamente). Esta espiral fue desarrollada por el matemático Teodoro de Cirene, utilizando el teorema de Pitágoras y añadiendo perpendicularmente a la hipotenusa un segmento de una unidad de medida, lo que forma triángulos cuyas hipotenusas son las sucesivas raíces √2, √3,√4, √5, etc.
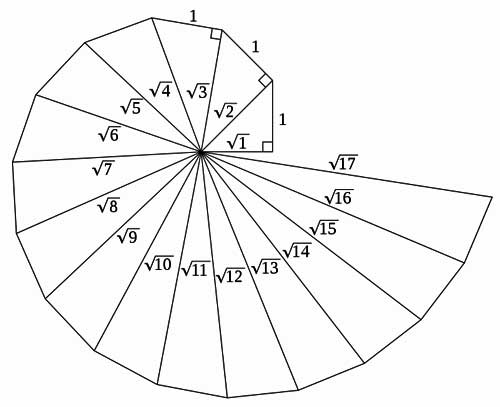
Construcción de la Espiral de Teodoro
Se inicia con un triángulo rectángulo isósceles, es decir, ambos catetos deben ser de longitud 1. Por el teorema de pitágoras, la hipotenusa de este triángulo es igual a raíz de 2. Luego se debe añadir un segmento de longitud 1 perpendicular a la hipotenusa del triángulo anterior. Por el teorema de pitágoras, la longitud de la hipotenusa de este segundo triángulo es raíz cuadrada de 3.
Es decir, el proceso de construcción consiste en estos dos pasos.
- Añadir un segmento de longitud 1, perpendicular a la hipotenusa del triángulo anterior.
- Hallar la hipotenusa del nuevo triángulo mediante el teorema de Pitágoras.
Se repite este proceso hasta llegar al triángulo de hipotenusa igual a raíz cuadrada de 17.
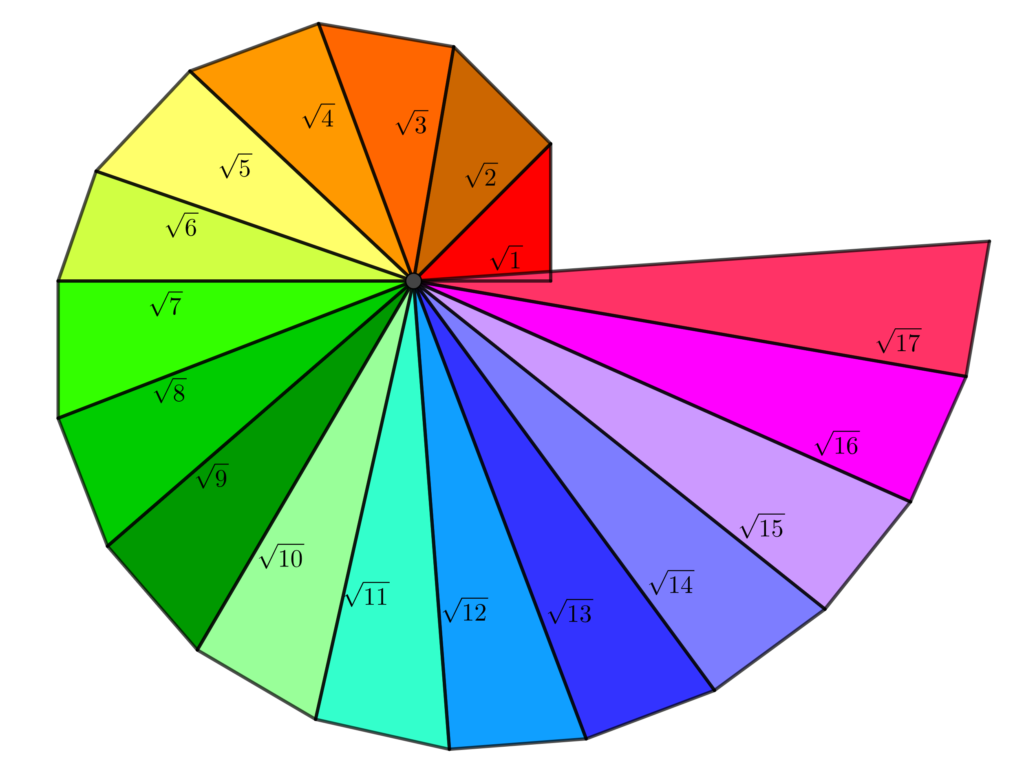
Te estarás preguntando: ¿Por qué Teodoro se detuvo en raíz de 17? La realidad es que se desconoce la causa por la cual no generalizó a números mayores y se detuvo en el 17. Sin embargo, algunos autores han conjeturado posibles razones:
- Autores han conjeturado que no quiso continuar porque significaba dar otra vuelta y superponer los dibujos (Paul Nahin: «An Imaginary Tale: The history of «)
- La versión de Van der Waerden («Science Awakening») dice que se detuvo al llegar a 17 porque la demostración concreta de la irracionalidad de 19 era más complicada, mientras que la de 18 no ofrecía interés por reducirse a la de casos anteriores (porque √18 = 3√2 ).
Aunque Teodoro finaliza esta espiral en el triángulo rectángulo de hipotenusa raíz de 17, se puede continuar con esta construcción añadiendo más triángulos rectángulos. En la siguiente imagen, por ejemplo, se llega hasta una hipotenusa de valor raíz de 100.
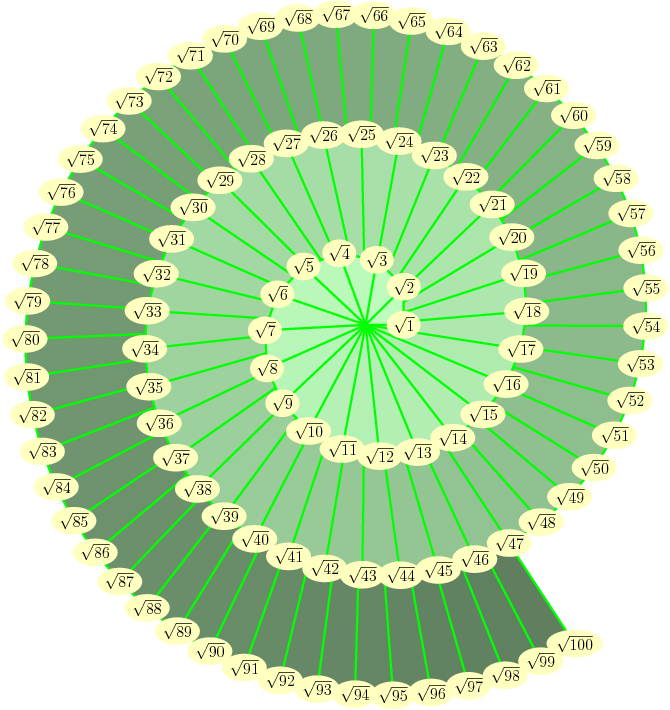
Propiedades importantes de la espiral de Teodoro
Hipotenusas
- La hipotenusa Hi, del triángulo i, es la raíz cuadrada de i+1, es decir Hi = √(i+1). Por ejemplo, la hipotenusa del triángulo 1, es h1 = √2, la del triángulo 2 es h2 = √3, y así sucesivamente.
- En el año 1958 Erick Teuffell demostró que no coincidirán dos hipotenusas si el proceso continúa indefinidamente.
- También demostró que si los catetos que miden una unidad de longitud se prolongan mediante una línea recta, nunca pasarán a través de ningún otro de los vértices de la espiral.
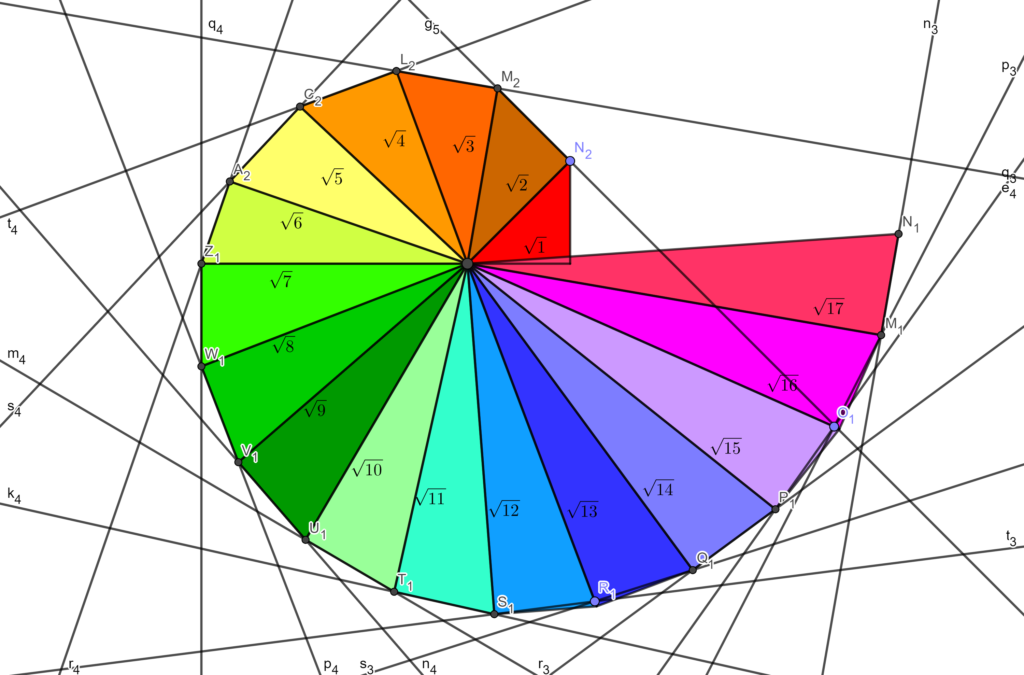
Ángulo del n-ésimo tríangulo de la Espiral
El ángulo del n-ésimo triángulo está dado por:


La utilidad de la espiral de Teodoro y su presencia en la naturaleza
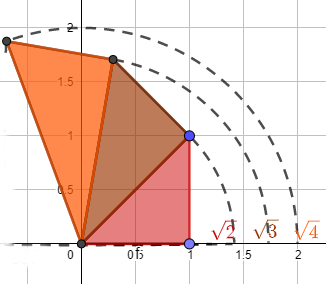
Útil como "calculadora visual" de raíces
Es una forma ingeniosa de visualizar las longitudes correspondientes a las raíces cuadradas de números naturales, en especial, aquellas raíces que resultan ser números irracionales, solo utilizando regla y compás.
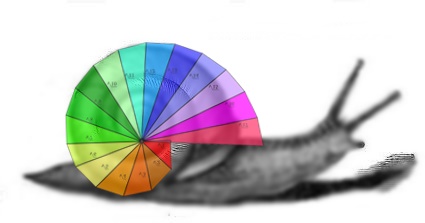
La espiral Pitagórica en el caracol terrestre y en la Via Lactea
Galileo dijo en su «Saggiatore» (1623) «La naturaleza está escrita en lenguaje matemático». En la siguiente imagen podemos observar como la forma geométrica de la espiral de Teodoro es semejante al caparazón de un caracol terrestre.
Nuestra galaxia, la Vía Láctea, tiene forma de espiral