Introducción
La recta de regresión lineal es una recta que es la que mejor se ajusta a los puntos dispersos. Estos puntos dispersos son la representación grafica de una posible relación entre las dos variables de estudio. Para entender esto, vamos a tomar un caso real y aplicaremos la recta de regresión.
El Geiser Old Faithful es la mayor atracción del Parque Nacional de Yellowstone. Este géiser lanza entre 3,700 y 8,400 galones de agua hirviendo desde alturas de 106 a 184 pies. Los turistas siempre desean ver al menos una erupción del famoso géiser.

Los guardabosques predicen las erupciones para ayudar a los turistas a no perdérselas. Los guardabosques registran las siguientes mediciones:
- Duración de la erupción (en segundos)
- El intervalo de tiempo posterior a una erupción (en minutos)
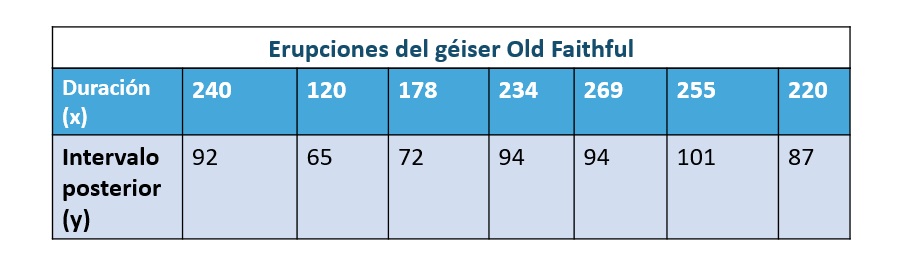
Diagrama de dispersión
Un diagrama de dispersión es una gráfica de datos apareados (x,y).
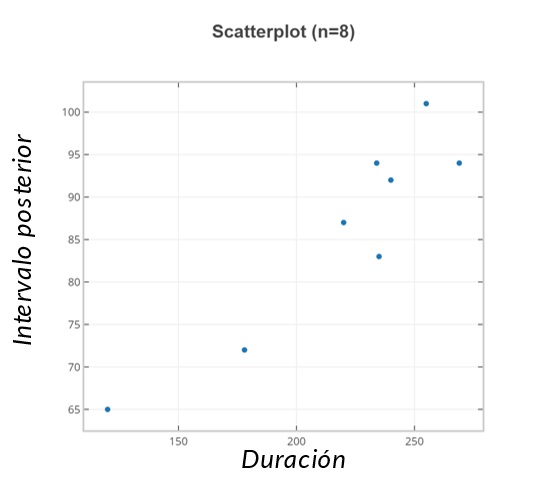
La recta de regresión lineal: La recta que mejor se ajusta
La variable y no está determinada por completo por la variable x, pero podemos encontrar una recta que es la que mejor se ajusta a los puntos dispersos llamada recta de regresión.
Dado un conjunto de datos muestrales apareados, la ecuación de regresión 𝑦 = 𝑏0 + 𝑏1𝑥 describe algebraicamente la relación entre las dos variables.
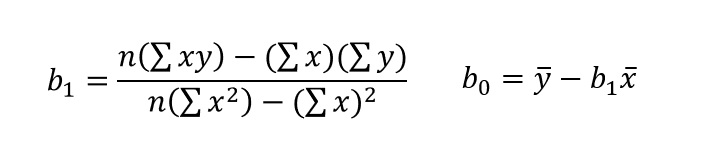
No te preocupes si no quieres realizar tantos cálculos a mano, solo accede a Statdisk.com, donde solo tienes que ingresar los datos apareados y tendrás todos los cálculos y gráficos que necesitas, si quieres aprender cómo usarla puedes ver este video.

Ejemplo
Si observamos una erupción de 180 segundos, podemos predecir el intervalo posterior a la erupción (hasta la siguiente erupción) al sustituir x =180 en la ecuación de regresión:
y = 34.7698 + 0.2341 (180) = 76.9 min.
El resultado indica que si una erupción tiene una duración de 180 segundos, el mejor intervalo de tiempo predicho después de la erupción es de 76.9 minutos.