Introducción
Desde pequeños nos enseñan a multiplicar números positivos, a memorizar la tabla de multiplicación y cuando llegamos a un nivel un poquito más alto, nos enteramos de que existen números negativos. Estos números son relacionados con algo muy cotidiano como son las deudas o pérdidas. Pero, ¿Cómo se multiplican? ¿Qué significa multiplicar dos números negativos? ¿Cómo se justifica la ley de los signos?
Este artículo tiene como propósito facilitar una información organizada y resumida sobre la justificación de la ley de los signos para todos aquellos que procuran un entendimiento histórico, matemático e intuitivo sobre esta regla.
Justificaciones de la ley de signos
Evolución del concepto de número negativo
Para entender las argumentaciones que se darán a continuación, debemos, por un momento, despojarnos del conocimiento matemático “refinado” que ya tenemos hoy día en el siglo XXI, donde todos aceptamos y comprendemos los números negativos. Recordemos que el concepto de número negativo no nació de manera acabada, universal y al mismo tiempo en todo el mundo, ni fue aceptado como un número por mucho tiempo.
Se sabe que ya para el año 600 d.C. los hindúes ya trabajaban con números negativos, sin embargo, en Europa los números negativos fueron introducidos por Leonardo de Pisa en su Liber Abaci (1202), pero no fueron aceptados como números hasta finales del siglo XVIII.

Por ejemplo, Blaise Pascal (1623-1662), consideraba absurdo restar de cero una cantidad positiva, Gerolamo Cardano (1501-1576) los consideraba símbolos sin significado real en el problema que trataba de resolver. René Descartes (1596-1650) llamaba falsas a las raíces negativas de las ecuaciones. Y era entendible, pues, para ellos un número siempre expresaba una cantidad, una cantidad existente. ¿Tenía sentido expresar la ausencia de cantidad, o algo menos que la ausencia de la cantidad, con un número?
La ley de los signos en el siglo III: Diofanto de Alejandría
En este tiempo, lo negativo estaba asociado a restas indicadas con solución positiva. Por ejemplo: (8−5)×(9−7).¿Cómo podríamos operar esta diferencia sin antes resolver dentro de los paréntesis? Podríamos hacer lo siguiente: (8−5)×(9−7)= 8(9)+8(−7)+(−5)(9)+(−5)(−7). Simplemente usamos la propiedad distributiva. Pero ¿Cómo resolvemos estos productos con signos distintos 8(−7), (−5)(9) y (−5)(−7)?

Diofanto de Alejandría, (el padre del álgebra), que también rechazaba los números negativos, hace alusión al producto de dos diferencias, y escribe una especie de ley de los signos.
“Lo que es lo que falta multiplicado por lo que es lo que falta da lo que es positivo; mientras que lo que es lo que falta multiplicado por lo que es positivo, da lo que es lo que falta” (Diofanto, Libro I, 250 d.C.). Esto podría ser entendido hoy día como:
(−)×(−)= + (Lo que es lo que falta multiplicado por lo que es lo que falta da lo que es positivo)
(−)×(+)= − (lo que es lo que falta multiplicado por lo que es positivo, da lo que es lo que falta)
No se ofrece una justificación, pero con esto podemos saber desde cuándo ya se venía pensando en la ley de los signos. Con esta ley dada por Diofanto podemos resolver (8−5)×(9−7) sin operar dentro de los paréntesis.
Justificación de la ley de los signos por Simon Stevin (1540-1620)
Stevin, primer matemático que aceptó los negativos como resultado de ecuaciones algebraicas, justifica la regla de los signos tomando como ejemplo (8−5)×(9−7) y comprobando cómo se llega al mismo resultado por dos caminos distintos:
Camino 1. Restando dentro de los paréntesis: (8−5)×(9−7)= 3×2 = 6
Camino 2. Aplicando la regla de los signos: (8−5)×(9−7)= 8(9)+8(−7)+(−5)(9)+(−5)(−7) =
72 + (−56) + (−45) + 35 = 6
Y para dar mayor credibilidad a la regla, ofrece una interpretación geométrica.

Demostración geométrica. Sea el lado AB = 8-5 (a saber AD−DB = 8−5). Después, AC = 9-7 (a saber AE-EC 9−7). Su producto será CB, o bien según la multiplicación DE 72 – EF 56 – DG 45 + GF 35. Los cuales demostraremos que son iguales a CB de esta forma.
El área total del cuadrado es 72 (DE), a esta área se le resta el área del rectángulo con área 56 (EF). También se le resta el área del rectángulo DG = 45, y se le añade el área GF porque se ha quitado dos veces. Lo que queda es CB = 6.
¿Qué es un número negativo y qué significa multiplicar dos negativos?

Estos números con signo negativo no eran coherentes con la idea que se tenía de cantidad y de número, pues los números eran lo que expresaban la cantidad; pero a medida que pasaba el tiempo las generalizaciones en álgebra fueron tomando lugar y así mismo los números negativos. Aceptar la existencia de cantidades menores que cero suponía una ruptura con la concepción absoluta del cero: aquello por debajo de lo cual no había nada.
Se entendió que para denotar las cantidades no era suficiente con determinar su valor absoluto, sino que también debía indicarse en qué sentido existía dicha cantidad. De manera que las cantidades que iban acompañadas del signo −, el cual actuaba como un adjetivo, modificaban el significado de las cantidades de la misma manera que un adjetivo modificaba el significado de un sustantivo.
Justificación de José Mariano Vallejo (1779-1846)
Vallejo, en su célebre Tratado Elemental de Matemáticas (1841 p. 185-199), define por extensión de la aritmética:
“Multiplicar en Álgebra es tomar una cantidad tantas veces como diga otra; y tomarla del mismo modo que diga se debe tomar”.

Pero la parte que más nos interesa de la definición de Vallejo es la última que dice “…y tomarla del mismo modo que diga se debe tomar”. Él explica a qué se refiere con esto diciendo:
“En el Álgebra no solo se atiende al valor absoluto de las cantidades, sino también a su modo de existir”.
En la multiplicación, el multiplicador nos indica cuantas veces debemos tomar el multiplicando, y el signo el modo con que le debemos tomar.
De manera que multiplicar a por b, es tomar a “b” tantas veces como indique “a”. El multiplicador nos indica cuantas veces debemos tomar el multiplicando, y el signo el modo con que le debemos tomar.
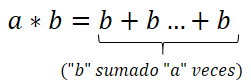
+2×3 = 3+3 = 6
El multiplicador +2 nos dice con sus unidades que tomaremos dos veces al multiplicando y su signo + nos dice que le tomemos como él sea, 3 es positivo, por tanto lo tomamos así mismo.
En cuanto a los signos en abstracto da: (+)×(+) = +
2×(−3)=
De igual manera, el multiplicador +2 nos dice con sus unidades que tomaremos dos veces al multiplicando, y su signo + nos dice que le tomemos como él sea, en este caso es -3
2×(−3)= −3 + (−3) = −3−3 = −6
En cuanto a los signos en abstracto da: (+)×(−)=−
−2×3 =
El multiplicador –2 nos indica con sus unidades que tomaremos dos veces al multiplicando y su signo – nos dice que le tomemos con su signo contrario a como él sea.
−2×3 = −3+(−3) = −3−3 = −6
En cuanto a los signos en abstracto da: (−)×(+)=−
Y por último si el caso fuera el siguiente: (−2)×(−3) =
-2 es el multiplicador y –3 el multiplicando. El multiplicador -2 nos indica con sus unidades que tomaremos dos veces al multiplicando con su signo cambiado. El multiplicando es negativo, luego le deberemos tomar positivamente. Por tanto:
(−2)×(−3) = 3+3 = 6
En cuanto a los signos en abstracto da: (−)×(−)=+
Justificación de ley de los signos por Leonhard Euler (1707-1783)
Euler interpretaba los negativos como deudas. En su libro Elementos de Algebra (1770, p. 35), presenta su justificación a la regla de los signos. Euler justificaba que (−)×(+)=− y que (+)×(−)= −, de la siguiente forma: Para Euler cualquier número negativo representaba una deuda. Por ejemplo: -3, podría estar refiriéndose a una deuda de tres centavos. Así -3×2, él lo interpretaba como deber -3 dos veces, así la deuda total era de -6. De esa manera justificaba que -3×(+2) = -6. En términos de signos; (−)×(+)= − , y considerando la conmutatividad de la multiplicación, (+)×(−)= −.
Por eso si multiplicamos -a por +b, obtenemos -ab.

Queda por resolver el caso en que − se multiplica por −; o, por ejemplo, −a por −b. Leonhard Euler argumenta lo siguiente:
“Dado que −a por +b da −ab, entonces −a por −b no puede producir el mismo resultado que -a por +b; sino que debe producir el contrario, esto es, +ab; consecuentemente tenemos la siguiente regla: multiplicar por – produce +, en la misma manera que + multiplicado por +”.
Justificación de MacLaurin (1698-1746) en coherencia con la propiedad distributiva
MacLaurin, en su Tratado de álgebra (1748), argumenta en coherencia con la propiedad distributiva, tomando las siguientes premisas como verdaderas:
- Que a−a = 0. Siendo «a» cualquier número.
- Cualquier número multiplicado por 0 es 0.
- Y que la ley distributiva se cumple en los números negativos.

Razona de la siguiente forma: Sean n, a, números positivos cualesquiera.
Si multiplicamos +n(a-a) = +na –na = 0. Tendré para el primer término +na, luego tendré para el segundo –na, ya que es preciso que los dos términos se destruyan.
Si multiplicamos –n(a-a) = −na +na = 0. Tendré −na para el primer término; luego tendré +na para el segundo, porque siempre hace falta que los dos términos se destruyan; luego – multiplicado por – da + en el producto.
Justificación de Laplace (1749-1827) en coherencia con la propiedad distributiva

Pierre-Simon Laplace, en sus lecciones de L’École normale de l’an III (1795, p. 62) interpreta, al igual que Euler, los números negativos como deudas y, al igual que MacLaurin, considera la propiedad distributiva.
Laplace observa:
“El producto de -a por +b, es -ab, ya que este producto no es mas que -a repetido tantas veces como unidades hay en b”.
Inmediatamente observamos que el producto −a(b−b)= 0 Porque b−b= 0 y −a×0 = 0; Siendo −ab el producto de −a por +b.
El producto de −a por −b, debe ser de un signo contrario, o igual a +ab, para destruirlo. Es decir, -a(b-b) = −ab +ab = 0
Justificación de Crowley y Dunn (1985) en coherencia con la propiedad distributiva
Una alternativa a la demostración de Laplace:

Modelizaciones intuitivas de la ley de los signos (2 ejemplos)
Los ejemplos no son demostraciones matemáticas pero sí son muy útiles para ayudar a comprender la razonabilidad de la regla y mostrar su consistencia con la experiencia cotidiana. A continuación se muestran dos ejemplos, uno basado en una interpretación geométrica dada por el matemático Félix Klein y el otro basado en el desplazamiento físico considerando la velocidad y el tiempo.
Modelización geométrica sobre rectángulos de Klein (1908)
La modelización de Klein se basa en la interpretación geométrica de Simon Stevin. Sea a>b, c>d; a−b y c−d son enteros positivos.
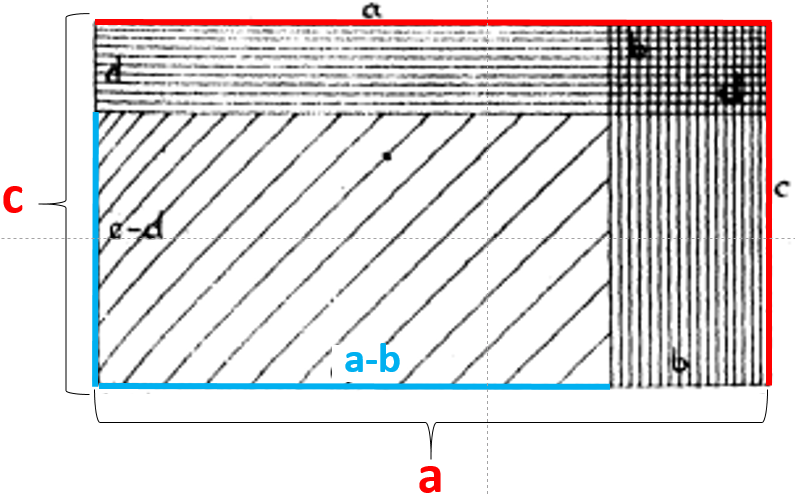
a y c son los lados del rectángulo completo. a−b y c−d son los lados del rectángulo con líneas diagonales.
El área del rectángulo completo está dado por: a×c (base por altura)
El área del rectángulo con líneas oblicuas está dado por: (a−b)×(c−d) (base por altura)
Para obtener el área del rectángulo con líneas oblicuas, sustraemos del rectángulo grande de área a×c, los rectángulos de área a×d y el b×c. El pequeño rectángulo del borde, de área bd, se debe añadir una vez, pues se ha sustraído dos veces.
En términos matemáticos: (a−b)×(c−d) = ac−ad−bc+bd
Si generalizamos un poco y prescindimos de a y c, es decir hacemos a = c = 0, se obtiene
La regla de los signos para de la multiplicación de números negativos: (−b)×(−d) = +bd
Modelización física sobre desplazamientos de Rey Pastor y Puig Adam (1946)
Esta modelización consiste en situar un objeto o persona en el cero de una recta.
- Desplazamiento hacia la izquierda = Movimiento en dirección negativa
- Desplazamiento hacia la derecha = Movimiento en dirección positiva
- Tiempo pasado = valor negativo
- Tiempo futuro = valor positivo
En esta modelización tomaremos como punto cero una estación de tren intermedia entre Madrid y Zaragoza. Si el tren se desplaza a 60km/h hacia Madrid, ¿Cuál será su distancia en las próximas 2 horas? +60×2 = +120
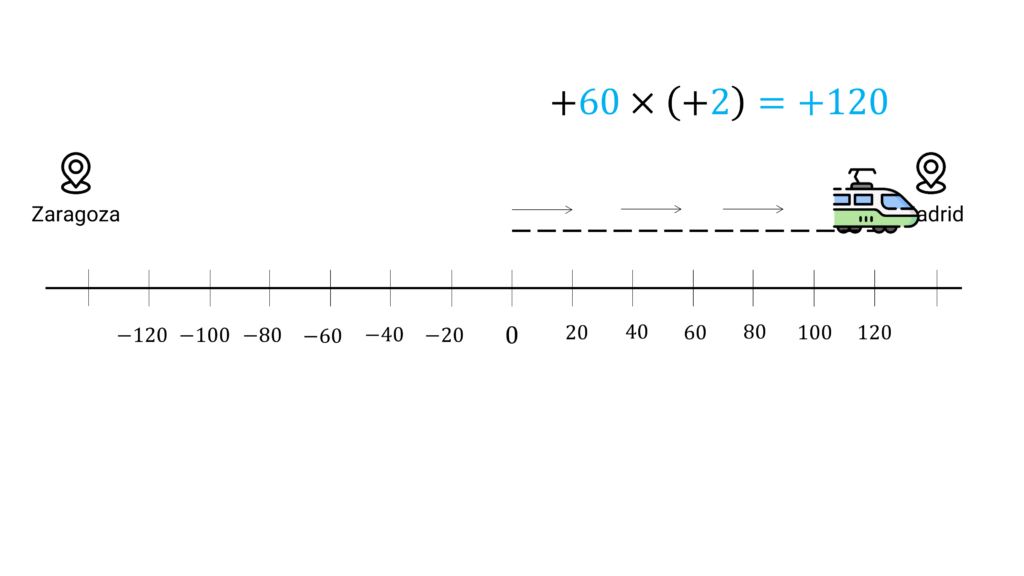
Por otro lado, hace 2 horas estaba a 120km de la estación de tren, pero del lado de Zaragoza. 60×(−2) = −120
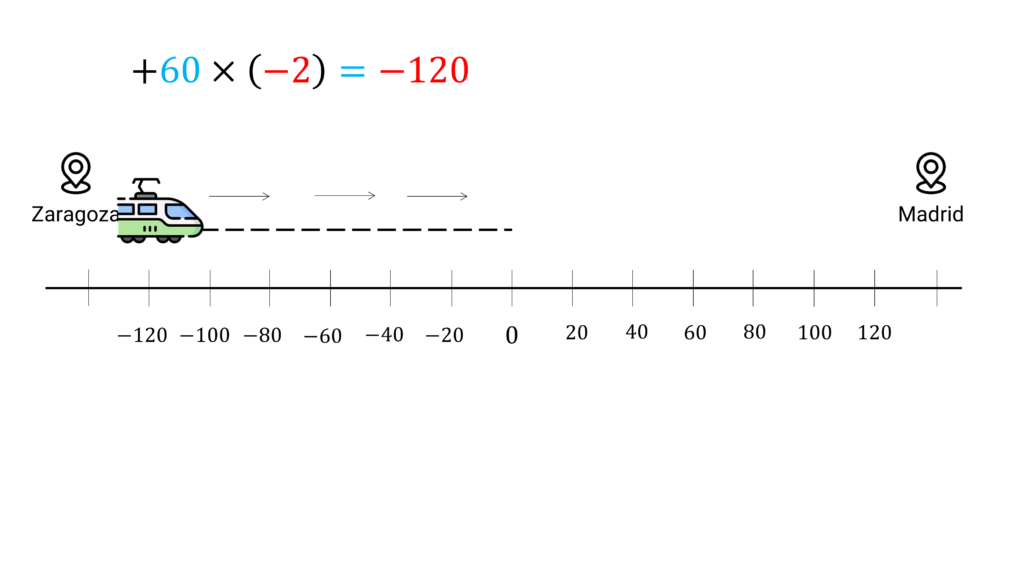
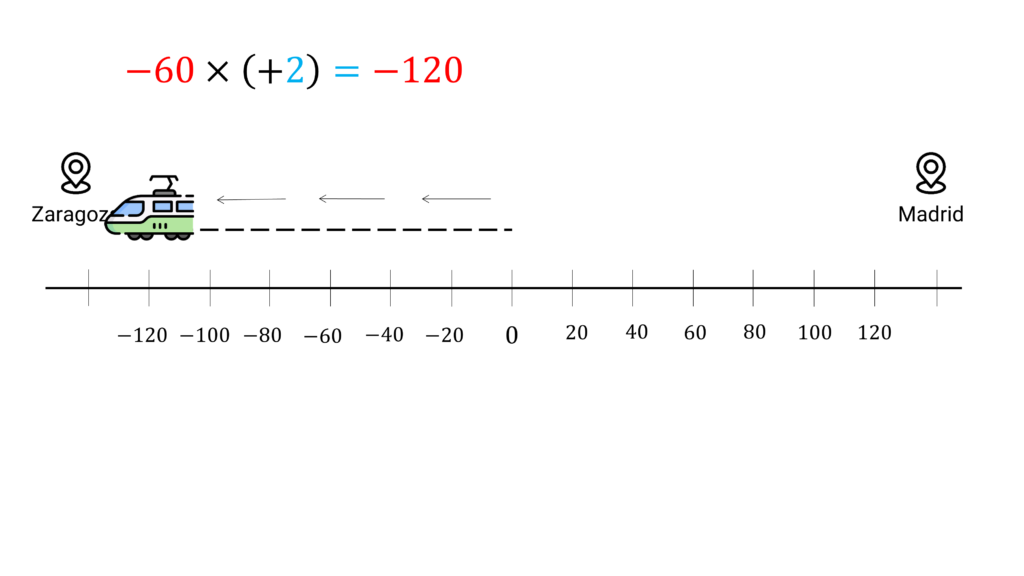
Si por el contrario el tren se dirige a Zaragoza (dirección negativa) a 60km/h, en 2 horas estaría a 120km del lado de Zaragoza. Es decir: (−60)×(+2)= −120
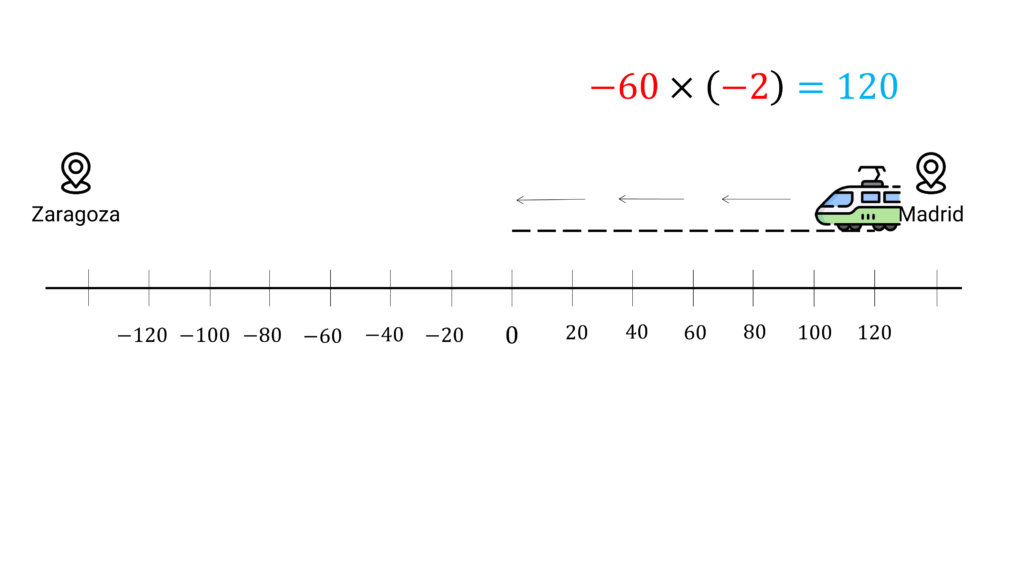
Si el tren se dirige a Zaragoza a 60km/h (dirección negativa), ¿Dónde se encontraba hace 2 horas? 120km en el lado de Madrid. Es decir; (−60)×(−2)= +120
Conclusión
Quizás te estés preguntando, ¿por qué tantas justificaciones? ¿Con una no es suficiente? Pues, como podrás a haber notado, algunas de las justificaciones son simples comprobaciones, otras se basan en la coherencia de propiedades que suceden en los enteros positivos pero que se asumen que también funcionan en los negativos, como el caso de la conmutatividad en las justificaciones dadas por Euler y Laplace, las modelizaciones son muy útiles para ayudar a comprender la razonabilidad de la regla, pero no son demostraciones matemáticas.
Cada justificación tiene sus debilidades, pero todas aportan una mayor comprensión a la regla de los signos, que muchas veces, ni siquiera se suele explicar en las escuelas.
Bibliografía
Crowley, M. y Dunn, K. (1985). On multiplying negative numbers. Mathematics teacher., 78 (4), 252-256.
Euler (1797). Elementos de Algebra. Traducido del francés con anotaciones críticas e históricas de M. Bernoulli, añadidas por M. De la Grange. Vol. I. London: J. Johnson.
GÓMEZ, B. (2001), “La justificación de la regla de los signos en los libros de texto: ¿Por qué menos por menos es más?” En Iniciación a la investigación en didáctica de la matemática, Universidad de Granada.
Klein, Félix (1908?). Matemática elemental desde un punto de vista superior. Vol I. Aritmética-Algebra-Análisis. (Traducción de Roberto Araujo) Madrid. Nuevas Gráficas
Laplace (1795). 1ª Lección de la Escuela Normal. En J. Dhombres (Ed.), L’École normale de l’an III. Leçons de Mathématiques. Laplace-Lagrange-Monge (pp. 9-141). Paris: Dunod. 1992.
Rey Pastor, J. y Puig Adam, P. (1946). Nociones de álgebra y trigonometría. Primera parte. Madrid. Imp. A. Aguado.
Stevin, S. (1585). L’arithmétique et la pratique de l’arithmétique. La Disme. En Girard (Ed.),Les oeuvres mathématiques. Leyden.1625 o 1634
Vallejo, J. M. (1841). Tratado Elemental de Matemáticas.escrito de orden de S. M. para uso de los caballeros seminaristas del seminario de nobles de Madrid y demás casas de educación del Reino. Cuarta edición corregida y considerablemente aumentada. Tomo I. Parte primera, que contiene la Aritmética y Álgebra. Madrid: Imp Garrayasaza.


This is a very good tip especially to those new to the blogosphere.
Short but very accurate info… Thanks for sharing this
one. A must read post!