Es probable que en la escuela hayas aprendido a calcular el Máximo Común Divisor de dos o más enteros utilizando la descomposición en factores primos. Sin embargo, en este artículo web, vamos a abordar un método diferente que se originó en la geometría griega, conocido como el algoritmo de Euclides. El objetivo es que puedas comprenderlo a través de una explicación visual y geométrica.
El algoritmo de Euclides fue desarrollado por el famoso geómetra griego Euclides del siglo IV a.C. Considerado “El padre de la geometría”, es ampliamente conocido por haber reunido y ordenado todos los conocimientos geométricos hasta ese momento en una obra titulada ELEMENTOS.
En la proposición 2 del libro VII de los Elementos, Euclides describe un algoritmo para buscar el Máximo Común Divisor (MCD) de dos números, que se puede interpretar, desde una perspectiva geométrica, como la mayor unidad de medida común de dos segmentos. En este artículo, vamos a explorar esta interpretación geométrica y a visualizar el algoritmo de Euclides.
La interpretación geométrica del MCD
Recordemos que el Máximo Común Divisor de varios números enteros es el número entero más grande por el cual son divisibles. Más exactamente: Sean a, b y c números enteros, si c es divisor común de a y b, y además es el de mayor valor absoluto, entonces c es el MCD de a y b, se denota como MCD(a,b) = c.
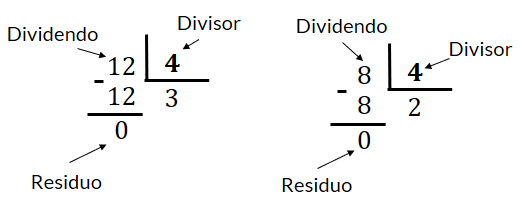
Por ejemplo: El Máximo Común Divisor de 12 y 8 es 4, ya que es el mayor número entero que divide de forma exacta a 12 y 8. Este se denota como MCD (12, 8) = 4
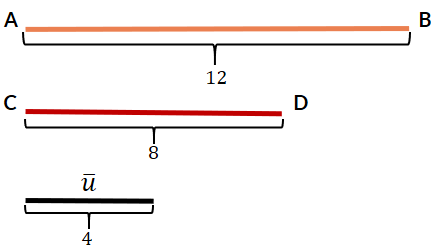
En la concepción griega los números eran entendidos, desde una perspectiva geométrica, como longitudes de segmentos geométricos. Así los números 12, 8 y 4 eran los segmentos AB, CD y u respectivamente:
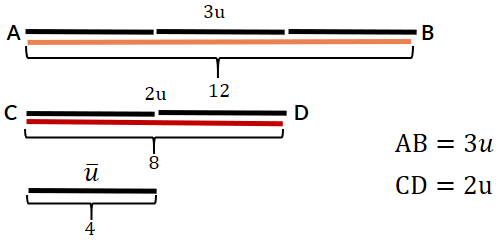
u es la mayor unidad de medida común que mide de forma exacta a AB y CD. Ya que AB = 3u y CD = 2u. Podríamos también tener los segmentos de longitud 1 y 2 respectivamente que también son medida común de AB y CD, pero el segmento u de longitud 4, es el mayor de todos.
Segmentos conmensurables
Si existe un tercer segmento u tal que AB y CD pueden medirse de forma exacta utilizando el segmento u como unidad entonces se dice que los segmentos AB y CD son conmensurables. El algoritmo de Euclides está diseñado para hallar ese segmento u.
AB y CD son conmensurables ya que existe un segmento u que los mide a ambos.
El algoritmo de Euclides
El algoritmo de Euclides es un procedimiento ordenado para hallar ese segmento u que mide a AB y CD. Describiremos los pasos de dicho algoritmo aplicándolo en un ejemplo concreto, calcularemos MCD(12,8).
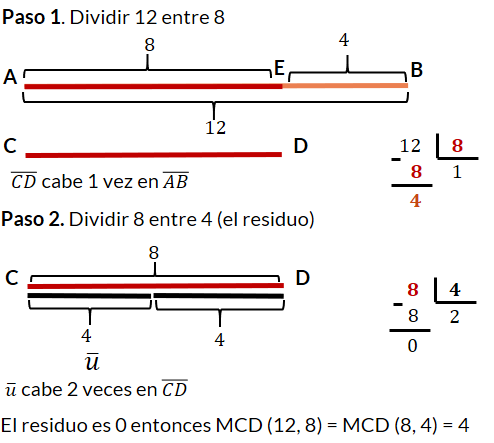
El algoritmo de Euclides consiste en dividir de forma sucesiva dividendo con el divisor, divisor con el residuo, hasta llegar a un residuo igual a cero. Luego el MCD es el último divisor utilizado en la divisiones sucesivas. El algoritmo de Euclides se puede resumir como sigue:

Ejemplo: Calcular MCD(57,12) utilizando el algoritmo de Euclides






Excelente. Bien explicado.
Éxitos.