Introducción
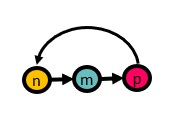
Lo que aparentemente parecía ser un chiste o una estrategia de la unión soviética contra Estados Unidos, se convirtió en un difícil problema matemático aún sin resolver, conocida como la conjetura de Collatz. El matemático alemán Lothar Collatz, Trató de representar las funciones aritméticas por grafos. Él unía n → m mediante un grafo, si f(n) = m. Los ciclos son especialmente interesantes, así que trató de definir funciones que generaran ciclos.
Un ciclo en teoría de grafos es un camino simple cerrado, es decir, una secuencia alternada de vértices distintos (bolitas de colores) y lados distintos (flechas) que comienza y termina en el mismo vértice.
La conjetura de Collatz
De esta forma, Lothar Collatz, experimentado con números enteros, funciones y grafos, observó en el año 1937 un fenómeno curioso, descubrió lo que parece ser una propiedad sencilla e inofensiva de los números enteros positivos:
i. Toma cualquier número entero positivo x
ii. Si x es par se divide entre dos.
iii. Si x es impar se multiplica por 3 y se suma 1
Llevando a cabo estas operaciones sucesivamente sobre el número resultante, el resultado final siempre alcanza el número 1, o por lo menos eso parece ser.
Ejemplo
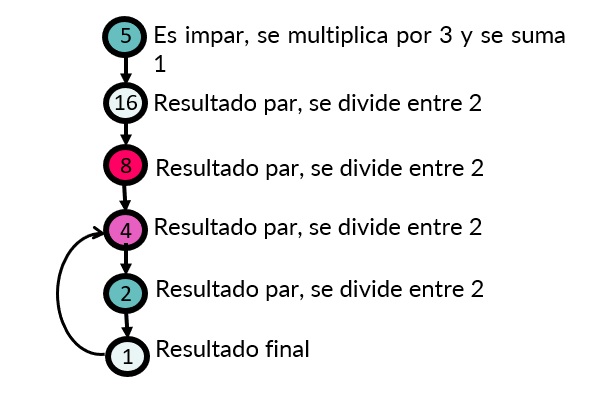
Experimentemos con el número 5. Recuerda las operaciones a aplicar según la paridad del número resultante.
Tomemos el número 5:
Función Collatz
Lo expresado anteriormente con palabras, se conoce como la función Collatz
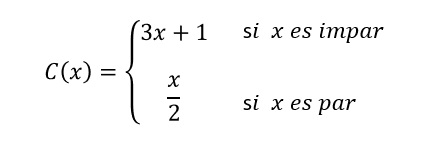
La Conjetura de Collatz dice que:
Aplicando reiteradamente la función de Collatz C a un número entero positivo cualquiera llegaremos al número 1.
Esta conjetura fue inicialmente tomada como un chiste o una broma, por su aparente simplicidad. Muchos pensaron que consistía en una estrategia soviética para desviar la atención de los investigadores matemáticos, debido a su simplicidad y difícil demostración.
Gráfica de trayectorias
La trayectoria de un numero x: Es la secuencia de sus iteraciones hacia adelante. También es llamada órbita del número x, para hacer referencia a las imágenes sucesivas al iterar la función.
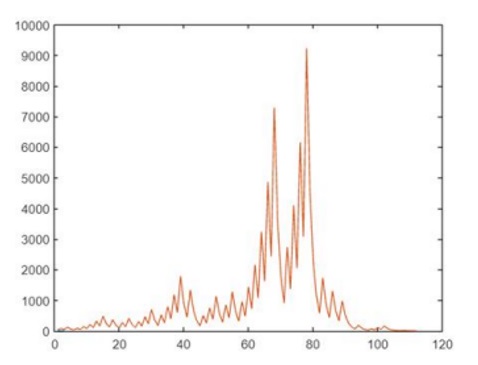
Iterando el número 27.
En el eje x se coloca la cantidad de pasos (iteraciones), en el eje y las imágenes de las iteraciones. Iterando el número 27 mediante la función Collatz, son necesarios 112 pasos para llegar a 1 y alcanza números tan grandes como 9232 en la iteración 78 antes de caer a 1.
Comportamiento caótico
No es posible determinar si la cantidad de pasos necesarios para que el número llegue a 1 obedece a si el número es grande o pequeño.
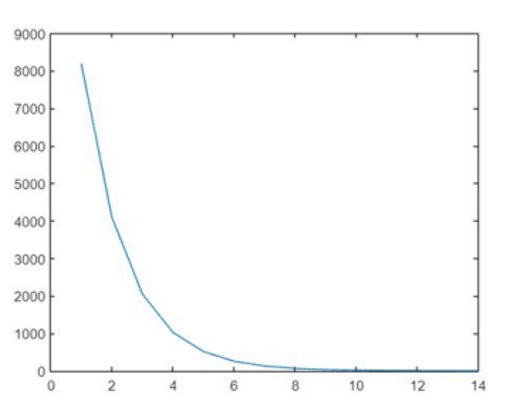
Iterando el número 8192 mediante la función Collatz, son necesarios 14 pasos para llegar a 1.
Al 27 le tomó 112 pasos
Los números que presentan una serie irregular de aumentos y disminuciones, se les llama “números de granizo” , ya que los granizos se forman por movimientos repetidos hacia arriba y hacia abajo como en una tormenta.
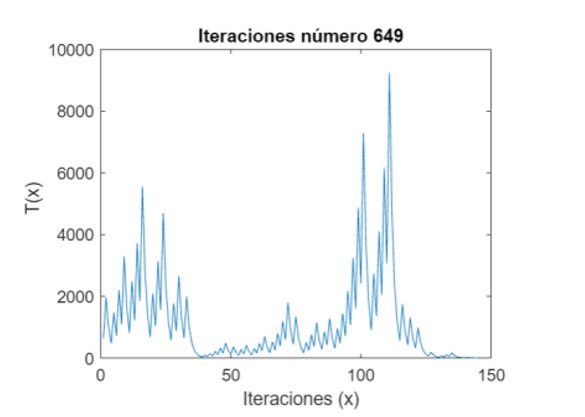
¿Qué pasa con Z-?
La conjetura está planteada considerando solo los números enteros positivos. Pero, ¿Pasará lo mismo con los enteros negativos? Se sabe que no es cierta en Z- , y basta un contraejemplo para refutarla. Por ejemplo, tomemos el -5:

Pero ¿por qué en los enteros negativos no se cumple la conjetura y en los positivos sí? Opina en los comentarios