Un siglo de mucha actividad matemática... y paradojas

El sigo XIX fue un periodo de intensa actividad matemática, algunos matemáticos intentaron formalizar toda la matemática a partir de la teoría de conjuntos de Georg Cantor. Uno de ellos fue Gottlob Frege quien publicó en 1893 su obra «Fundamentos de la Aritmética Vol. 1» donde creaba una axiomática de la teoría de conjuntos desde donde pretendía fundamentar toda la matemática de forma lógica y completa. En ese intento se destaparían muchos problemas y paradojas matemáticas que atentarían contra tales trabajos, como lo fue la paradoja de Russell que trataremos en este artículo.
Gottlob Frege, utilizó el axioma de comprensión para definir los conjuntos. Este axioma afirma que: «existe cualquier conjunto cuyos elementos están definidos por una propiedad».
Ejemplo: Notación por comprensión
Consiste en expresar una propiedad que cumplan todos los elementos del conjunto. En este ejemplo, el conjunto P, es el conjunto de los números pares.
Ejemplo: Notación por extensión
Un conjunto está definido por extensión si enumeran o enlistan los elementos que pertenecen a dicho conjunto. En este ejemplo, tomamos el mismo conjunto P anteriormente definido mediante por comprensión, ahora lo hemos definido mediante extensión y los puntos suspensivos indican que existen más elementos siguiendo el mismo patrón observado.
La paradoja de Bertrand Russell
El famoso filósofo y matemático Bertrand Russell, le escribió a Frege en el año 1902 realizándole la siguiente pregunta:

Es muy probable que no hayas entendido la pregunta a la primera o te ha dejado un poco confundido lo que parece ser un trabalenguas, pero tranquilo, este artículo tiene el propósito de ayudarte a asimilarla. Para entender la paradoja necesitamos primero comprender qué son los conjuntos singulares y normales.
Tipos de conjuntos
De forma muy primitiva, intuitiva y sin mucho cuidado, podemos definir un conjunto como: una colección de elementos. Todo conjunto debe caer en una de estas dos categorías: normal o singular, deja te explico qué es un conjunto normal y conjunto singular.
Conjuntos normales: Es todo conjunto que no se contiene así mismo.

Conjuntos singulares: Es todo conjunto se contiene así mismo.

La Paradoja de Russell: ¿El conjunto M es singular o normal?
Consideremos el conjunto M, conformado por todos los conjuntos que no se contienen así mismos:
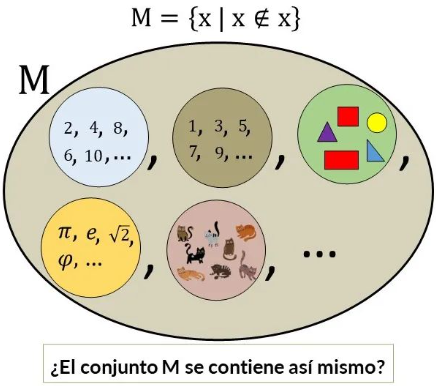
La pregunta es: ¿El conjunto M se contiene así mismo?
Si decimos que NO se contiene así mismo, entonces por definición debe ir dentro de M, (dentro de sí mismo, pues es el conjunto formado por los conjuntos que no se contienen).
Si decimos que SÍ se contiene así mismo, entonces por definición NO debe ir dentro de M, pues M es el conjunto formado solo por aquellos conjuntos que no se contienen así mismos
Este bucle, es la Paradoja de Russell, «M pertenece así mismo si y solo si M no pertenece así mismo». Una locura, una contradicción, una paradoja y un golpe bajo contra la aparente perfección de la que tanto alardeaba la matemática.
Russell se sentaba todas las mañanas frente a una hoja de papel en blanco, sin poder escribir nada. Pero tranquilos, les tengo buenas noticias, la solución de la paradoja fue hallada hasta 1906, con la elaboración de la Teoría de tipos en manos de Bertrand Russell y Alfred North Whitehead expuesta en un conjunto de tres libros con el título «Principia mathematica» publicados entre 1910 y 1913, acabando así con la contradicción.
¿Qué te parece esta paradoja?, ¿La habías escuchado? Déjanos tu comentario, te leemos.




