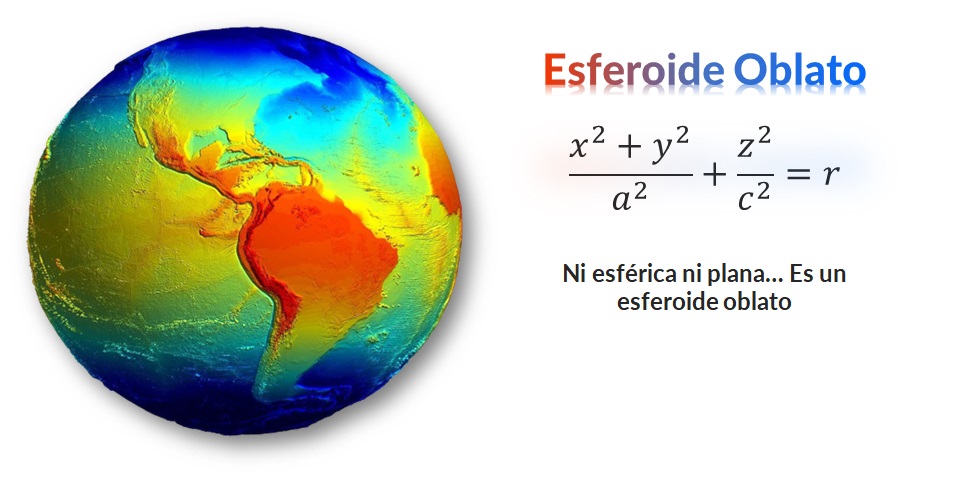
Introducción
Cualquier persona con un nivel promedio de educación sabe que la Tierra es cuasi-esférica; sin embargo, gracias a las teorías conspirativas que pululan en las redes sociales, han surgido numerosos grupos que han desempolvado el terraplanismo para defenderlo. Resulta muy irónico que esto suceda en el siglo XXI, pues, ya para el siglo III antes de Cristo, un genio de Grecia tenía muy claro que la Tierra era esférica y fue capaz de medir la tierra con un palo.
Por lo menos ya para los tiempos clásicos (siglo V a.C. – siglo II a.C.), contrario a lo que se suele pensar, los antiguos pensadores y genios ya concebían la Tierra como una esfera y no como una superficie plana. Por ejemplo, Aristóteles (siglo IV a.C.), en su obra “Sobre el cielo», dio una razonada explicación de por qué la Tierra era una esfera.

Pero la hazaña sorprendente fue realizada por un matemático y geógrafo griego llamado Eratóstenes de Cirene (Cirene 276 a.C. – Alejandría 194. a.C.) , también conocido por ser director de la famosa Biblioteca de Alejandría. La hazaña fue: ser la primera persona en calcular la circunferencia de la Tierra.
¿Cómo midió la Tierra?
Eratóstenes sabía que en Siena (hoy Asuán, Egipto) el día de solsticio de verano los objetos verticales no proyectaban sombra alguna, dando a entender que los rayos de luz del Sol son perpendiculares al suelo llano de la ciudad de Siena.

Un día de solsticio de verano, Eratóstenes se desplazó a la ciudad de Alejandría, a 800 km de Siena. Con un palo colocado rectamente contra el piso midió:
- La sombra que proyectaba el palo sobre el suelo
- La longitud del palo
Hace 2200 años, no existía el cálculo trigonométrico. Por lo que es probable que Eratóstenes haya medido el ángulo β con un compás. Pero nosotros podemos usar la función tangente y su inversa para obtener el ángulo exacto.
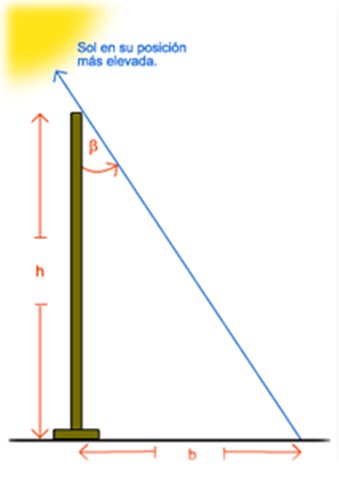
El ángulo que obtuvo fue de 7.2 grados. Por ángulos entre paralelas (rayos de luz) y una secante (palo subtendido), supo que el ángulo 7.2 grados era el ángulo central o la abertura que había entre Siena y Alejandría.
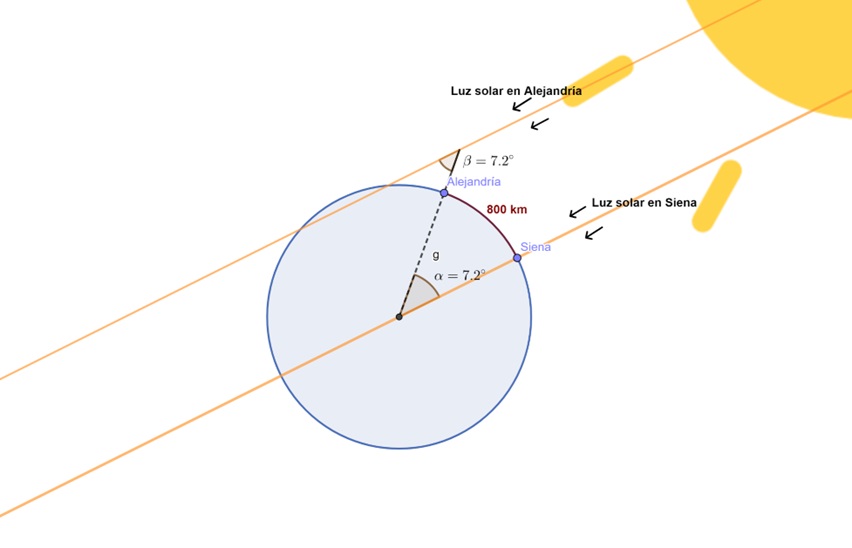
Además, 7.2 grados es 1/50 de 360 grados. Por lo que con una simple regla de tres podemos extrapolar el resultado a la circunferencia completa (360º):
7.2 → 800 km
360 → x
x = 50 (800km) = 40,000 km
En conclusión, Eratóstenes obtuvo un resultado casi igual al que se tiene actualmente: 40,008 km, es decir, un error de menos del 1 %.